Une figure fractale est un objet mathématique, telle une courbe ou une surface, dont la structure est invariante par changement d'échelle
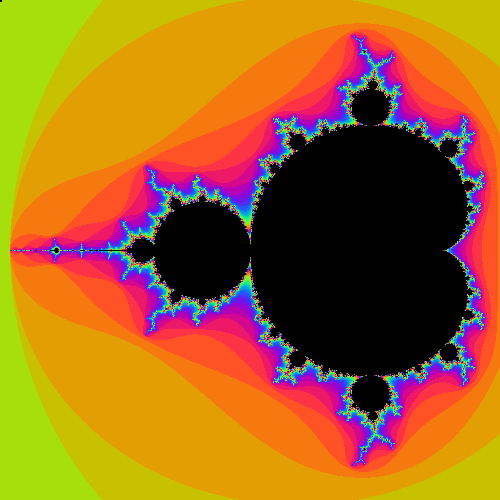
la figure fractale la plus connue est l'ensemble de Mandelbrot :
Passioné par ces figures autorépliquantes, J'ai réalisé deux programmes :
la figure fractale la plus connue est l'ensemble de Mandelbrot :

Ensemble de Mandelbrot.
| $z_0=x+i y$ | |
| $z_{n+1}=z_n^2+c$ | |
| $c=x+i y$ | $c=a+i b$ |
|

|
| lien vers l'Ensemble de Mandelbrot | lien vers l'Ensemble de Julia/ |
| Algorthime Matlab | |
function iter=fractale_mandelbrot(x,y,Nbmax_iter) zn=x+i*y; for iter=0:Nbmax_iter zn=zn^2+x+i*y; if abs(zn)>2 break end end end |
function iter=fractale_julia(x,y,a,b,Nbmax_iter) zn=x+i*y; for iter=0:Nbmax_iter zn=zn^2+a+i*b; if abs(zn)>2 break end end end |
| Algorthime Python | |
def Mandelbrot(x,y,max_iter): z_x=x z_y=y for nb_iter in range(max_iter+1): z_tx=z_x z_x=(z_x*z_x)-(z_y*z_y)+x z_y=2*z_tx*z_y+y if (z_x*z_x+z_y*z_y)>4: break return nb_iter |
def Julia(x,y,a,b,max_iter): z_x=x z_y=y for nb_iter in range(max_iter+1): z_tx=z_x z_x=(z_x*z_x)-(z_y*z_y)+a z_y=2*z_tx*z_y+b if (z_x*z_x+z_y*z_y)>4: break return nb_iter |
| Programme complet : içi | Programme complet : içi |
- Fractale plot
- Tree Fractale
Ce logiciel trace des courbes de Koch dans la figure connue est le flocon de Koch, qui à la caractéristique d'avoir une surface finie mais un périmètre qui tant vers l’infini.

flocon de Koch.
L'arbre de Pythagore est une fractale plane construite à l'aide de carrés. Elle porte le nom de Pythagore car chaque triplet de carrés en contact enclôt un triangle rectangle, une configuration traditionnellement utilisée pour illustrer le théorème de Pythagore.
 Arbre de Pythagore Multicolor |
 Arbre de Pythagore rouge |
On peut aussi remplacer les carrés par des rectangles et les triangles rectangle par des rectangles quelconque.
 Arbre hypercube |
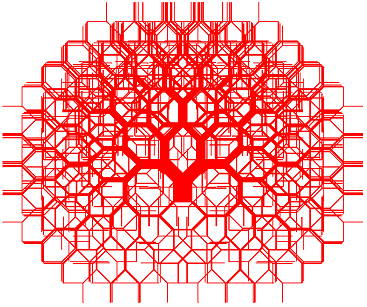 Arbre Cosmique |